Explanation of Encryption Keys
Table of Contents
Introduction
Encryption keys are a crucial element for securely protecting data. This page explains the various types of encryption keys, their uses, and how they work. Encryption technology forms the foundation of modern security systems and is used in many fields, including internet communication, data protection, and authentication.
Basics of Encryption
What is Encryption?
Encryption is the process of converting information so that it cannot be read by third parties. Encrypted data can only be converted back to the original information by someone who has the appropriate key. Encryption is used to protect confidential information, ensure communication security, and verify data integrity.
History of Encryption
The history of encryption dates back to ancient times. Early ciphers were simple methods like substituting or rearranging letters. For example, the Caesar cipher of ancient Rome was a simple method of shifting the alphabet by a certain number of places.
Modern encryption has become more complex with the development of computers, and powerful cryptographic methods based on mathematical algorithms have been developed. The breaking of the Enigma machine's code during World War II greatly contributed to the development of modern cryptography.
Role of Encryption Keys
An encryption key is a secret value used in conjunction with a cryptographic algorithm. The key controls the encryption and decryption process, and using different keys with the same algorithm produces different results.
The main roles of an encryption key are as follows:
- Encrypting and decrypting data
- Generating and verifying digital signatures
- Authentication and identification
- Ensuring data integrity
Key Length and Security
The length of an encryption key is directly related to the strength of the encryption. The longer the key, the more resistant it is to brute-force attacks.
For example, a 128-bit key has 2128 (approximately 3.4×1038) possible combinations, making a brute-force attack impractical with current computer technology. Commonly used key lengths are as follows:
- Symmetric-key cryptography (e.g., AES): 128 bits, 192 bits, 256 bits
- RSA (Public-key cryptography): 2048 bits, 3072 bits, 4096 bits
- Elliptic Curve Cryptography (ECC): 256 bits, 384 bits, 521 bits
As computer processing power improves, the recommended key lengths gradually increase. It is important to select an appropriate key length according to security requirements.
Encryption Key Management
Encryption key management is one of the most critical elements of an entire security system. Without proper key management, even the strongest encryption algorithm is rendered meaningless.
The main aspects of key management include:
- Key generation: Using an unpredictable random number generator to create keys
- Key storage: Storing keys securely (e.g., in a Hardware Security Module)
- Key distribution: Distributing keys to relevant parties in a secure manner
- Key rotation: Regularly updating keys to maintain security
- Key destruction: Securely destroying keys that are no longer needed
Symmetric-key Cryptography
What is Symmetric-key Cryptography?
Symmetric-key cryptography (or symmetric encryption) is a cryptographic system that uses the same key for both encryption and decryption. The sender and receiver must share the same key in a secure manner beforehand. This method is faster than public-key cryptography and can efficiently encrypt large amounts of data.
How Symmetric-key Cryptography Works
The basic mechanism of symmetric-key cryptography is as follows:
- The sender and receiver share the same key in a secure manner beforehand.
- The sender encrypts the message using this shared key.
- The encrypted message is sent to the receiver.
- The receiver decrypts the message using the same shared key.
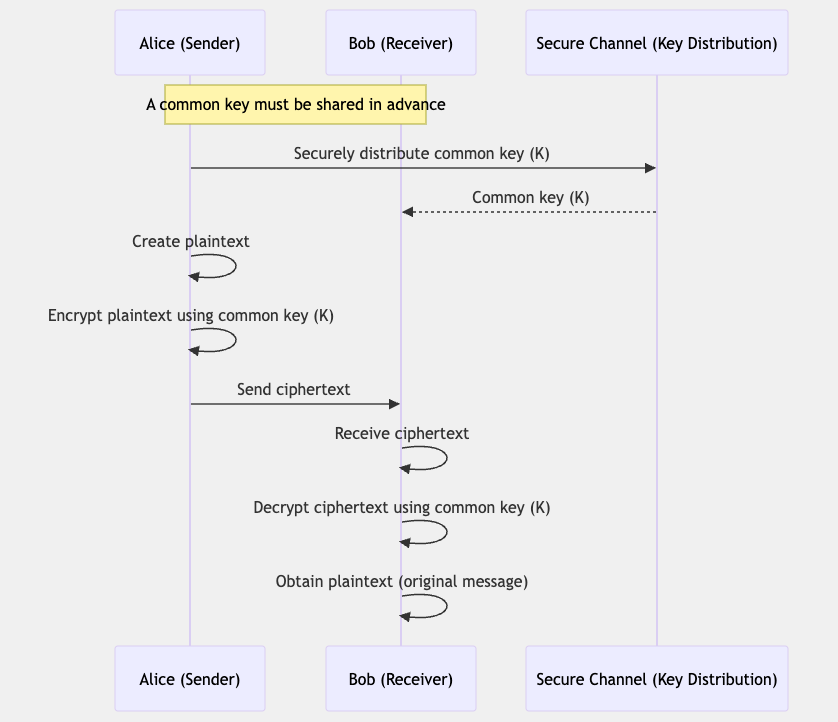
The biggest challenge with symmetric-key cryptography is how to securely share the key. To solve this problem, hybrid systems that combine it with public-key cryptography are often used.
Types of Symmetric-key Ciphers
Block Ciphers
Block ciphers encrypt data in fixed-size blocks. For example, AES uses a block size of 128 bits (16 bytes). If the data is larger than the block size, it is divided into multiple blocks for processing.
Main features of block ciphers:
- Process data in fixed-size blocks
- The same plaintext block encrypted with the same key results in the same ciphertext
- Various modes of operation are available (e.g., ECB, CBC, CTR, GCM)
Stream Ciphers
Stream ciphers encrypt data continuously, one bit or one byte at a time. Encryption is performed by a bitwise XOR operation between the plaintext and a pseudorandom sequence (keystream) generated from the key.
Main features of stream ciphers:
- Process data continuously
- Low memory usage and high-speed processing
- Suitable for real-time communication and streaming data
Major Symmetric-key Algorithms
AES (Advanced Encryption Standard)
AES is currently the most widely used symmetric-key algorithm. It was standardized by the U.S. National Institute of Standards and Technology (NIST) in 2001. It supports a block size of 128 bits and key lengths of 128, 192, or 256 bits.
AES combines high security and efficiency and is used in many security protocols and applications.
DES (Data Encryption Standard)
DES is an early symmetric-key algorithm standardized in 1977. It has a block size of 64 bits and an effective key length of 56 bits. Its security is insufficient with modern computing power, and it is not recommended for use in new systems.
3DES (Triple DES)
3DES is a cryptographic algorithm that enhances security by applying the DES algorithm three times. The effective key length is 112 or 168 bits. It is slower than AES and is gradually being replaced.
ChaCha20
ChaCha20 is a fast stream cipher, particularly efficient on mobile devices and in environments without hardware acceleration. It uses a 256-bit key and a 64-bit nonce (initialization vector). It is used in protocols like TLS.
Block Cipher Modes of Operation
Block cipher modes of operation define how to securely encrypt large amounts of data using a single block cipher. The main modes of operation include:
ECB (Electronic Codebook) Mode
This is the simplest mode of operation, encrypting each block independently. The same plaintext block results in the same ciphertext block, so patterns are preserved. For security reasons, it is not recommended for general use.
CBC (Cipher Block Chaining) Mode
Before encrypting each block, an XOR operation is performed with the ciphertext of the previous block. An initialization vector (IV) is used for the first block. CBC mode is more secure than ECB mode because the same plaintext block results in different ciphertext.
CTR (Counter) Mode
Encryption is performed by encrypting a counter value and then XORing the result with the plaintext. This effectively allows a block cipher to be used as a stream cipher. It allows for parallel processing and is fast.
GCM (Galois/Counter Mode)
This is a mode that adds authentication functionality to CTR mode. It generates a Message Authentication Code (MAC) simultaneously with encryption, ensuring both data confidentiality and integrity. It is used in many security protocols such as TLS.
Advantages and Challenges of Symmetric-key Cryptography
Advantages
- Processing Speed: Very fast compared to public-key cryptography
- Resource Efficiency: Can run with fewer computer resources
- Cryptographic Strength: Stronger than public-key cryptography for the same key length
Challenges
- Key Distribution Problem: A secure method for sharing the key is required
- Key Management Complexity: To achieve secure communication among n users, n(n-1)/2 keys are needed
- Lack of Non-repudiation: Since the sender and receiver have the same key, it's impossible to prove who initiated the communication
Public-key Cryptography
What is Public-key Cryptography?
Public-key cryptography (or asymmetric cryptography) is a cryptographic system that uses different keys for encryption and decryption. Each user has a "public key" and a "private key" pair. The public key can be used by anyone, but the private key is known only to the owner. This method allows for encrypted communication without prior secure key sharing.
How Public-key Cryptography Works
The basic mechanism of public-key cryptography is as follows:
- Each user generates a public key and a private key pair.
- The public key is made available to anyone.
- The private key is kept secret by the owner and never shared with anyone.
- To send a message, the sender encrypts the message with the receiver's public key.
- The encrypted message can only be decrypted with the receiver's private key.
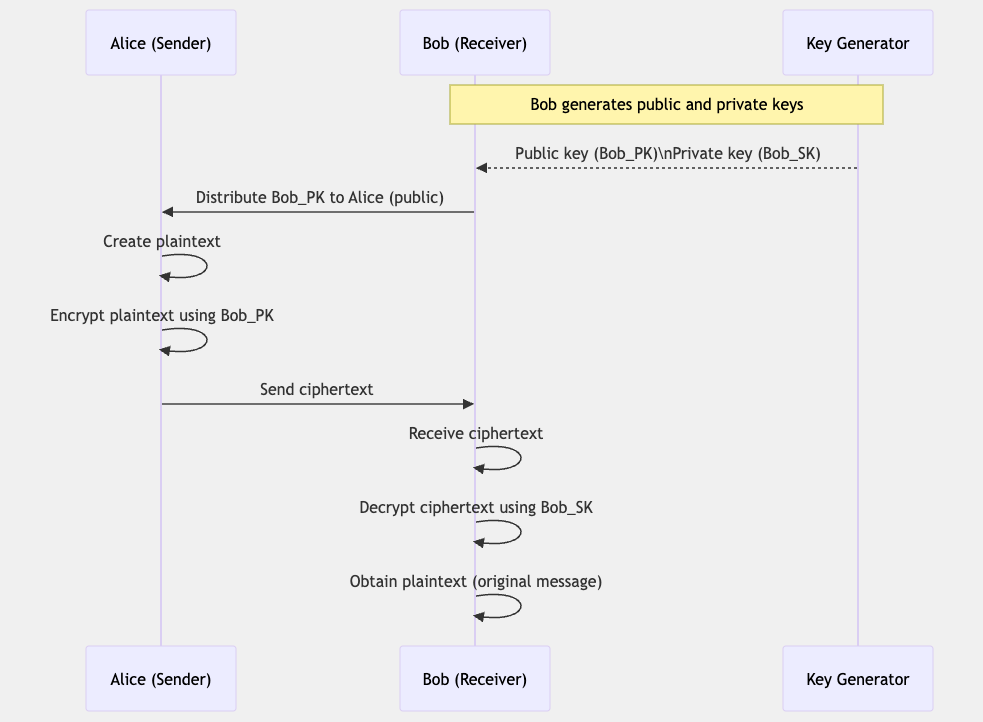
An important feature of this method is that data encrypted with a public key can only be decrypted with the corresponding private key. Also, data signed with a private key can be verified with the corresponding public key.
Major Public-key Algorithms
RSA (Rivest-Shamir-Adleman)
RSA is one of the most widely used public-key algorithms. It is based on the difficulty of factoring the product of large prime numbers. RSA can be used for encryption, decryption, and digital signatures.
An RSA key length of 2048 bits or more is generally recommended, with 4096 bits also used depending on security requirements.
Elliptic Curve Cryptography (ECC)
Elliptic Curve Cryptography is based on the difficulty of the discrete logarithm problem on elliptic curves. Compared to RSA, it can achieve a similar level of security with a shorter key length. For example, 256-bit ECC provides security equivalent to 3072-bit RSA.
ECC is particularly useful on mobile devices and systems with constraints.
ElGamal
ElGamal is a public-key algorithm based on the discrete logarithm problem. It is mainly used for encryption and can also be applied to digital signatures.
Digital Signatures
A digital signature is an important application of public-key cryptography. Digital signatures allow for the verification of the message sender's identity (authentication) and the detection of message tampering (integrity).
The basic mechanism of a digital signature is as follows:
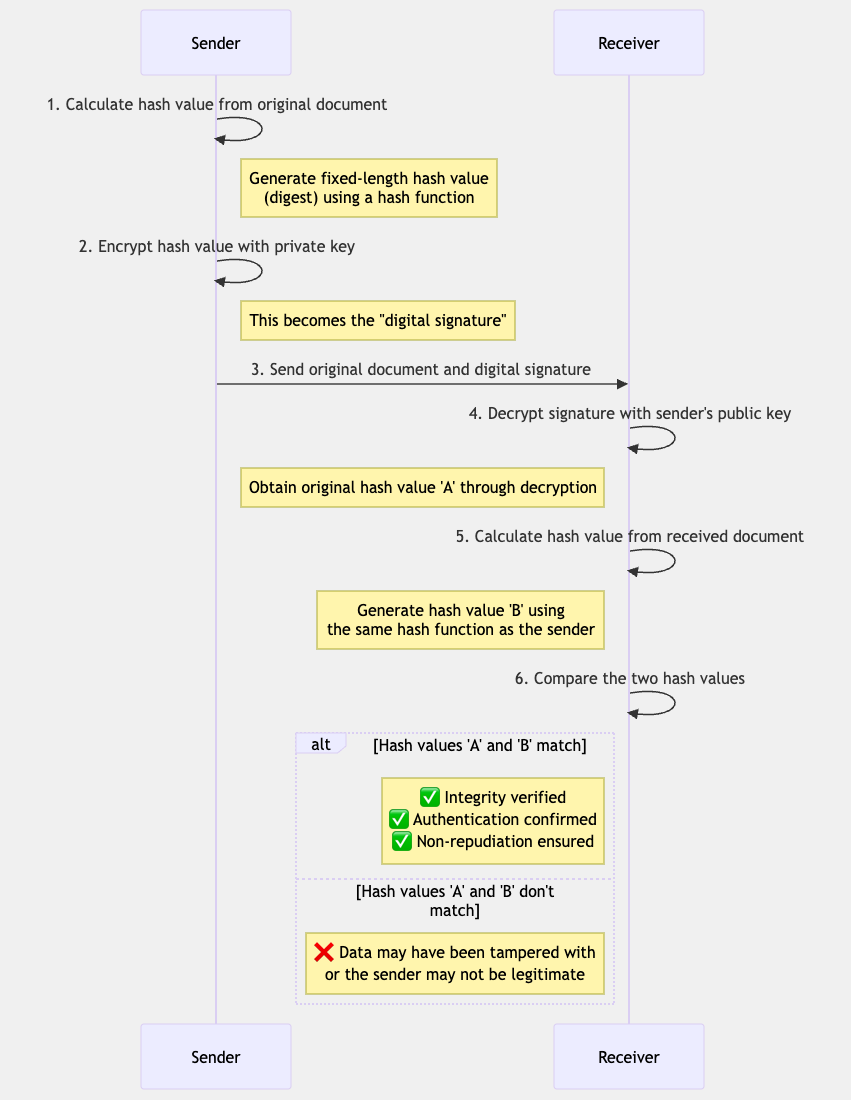
PKI (Public Key Infrastructure)
Public Key Infrastructure (PKI) is a framework for the practical operation of public-key cryptography. PKI ensures that a public key truly belongs to a specific individual or organization by issuing, managing, and validating digital certificates.
The main components of PKI include:
- Certificate Authority (CA): A trusted third-party organization that issues digital certificates and certifies the owner of a public key.
- Registration Authority (RA): An authority that verifies the identity of a certificate applicant and requests the CA to issue a certificate.
- Digital Certificate: An electronic document that contains a public key and its owner's information, digitally signed by a CA.
- Certificate Revocation List (CRL): A list of certificates that have been revoked before their expiration date.
PKI is used in many applications, such as HTTPS connections in web browsers, encryption and signing of emails (S/MIME), and code signing.
Advantages and Challenges of Public-key Cryptography
Advantages
- No Prior Key Sharing Required: Encrypted communication is possible even over insecure communication channels.
- Simplified Key Management: Fewer keys are required for n users (n pairs vs. n(n-1)/2 keys).
- Enables Digital Signatures: Allows for authentication and integrity.
- Non-repudiation: The sender cannot later deny having sent the message.
Challenges
- Processing Speed: Computationally more expensive than symmetric-key cryptography.
- Key Length: Requires longer keys to achieve the same level of security.
- Public Key Trustworthiness: It is necessary to verify that a public key truly belongs to a specific individual or organization (the role of PKI).
Hybrid Cryptosystems
A hybrid cryptosystem is a system that combines the advantages of public-key cryptography and symmetric-key cryptography. Typically, public-key cryptography is used to securely exchange a symmetric key (session key), and that symmetric key is then used to encrypt the actual data.
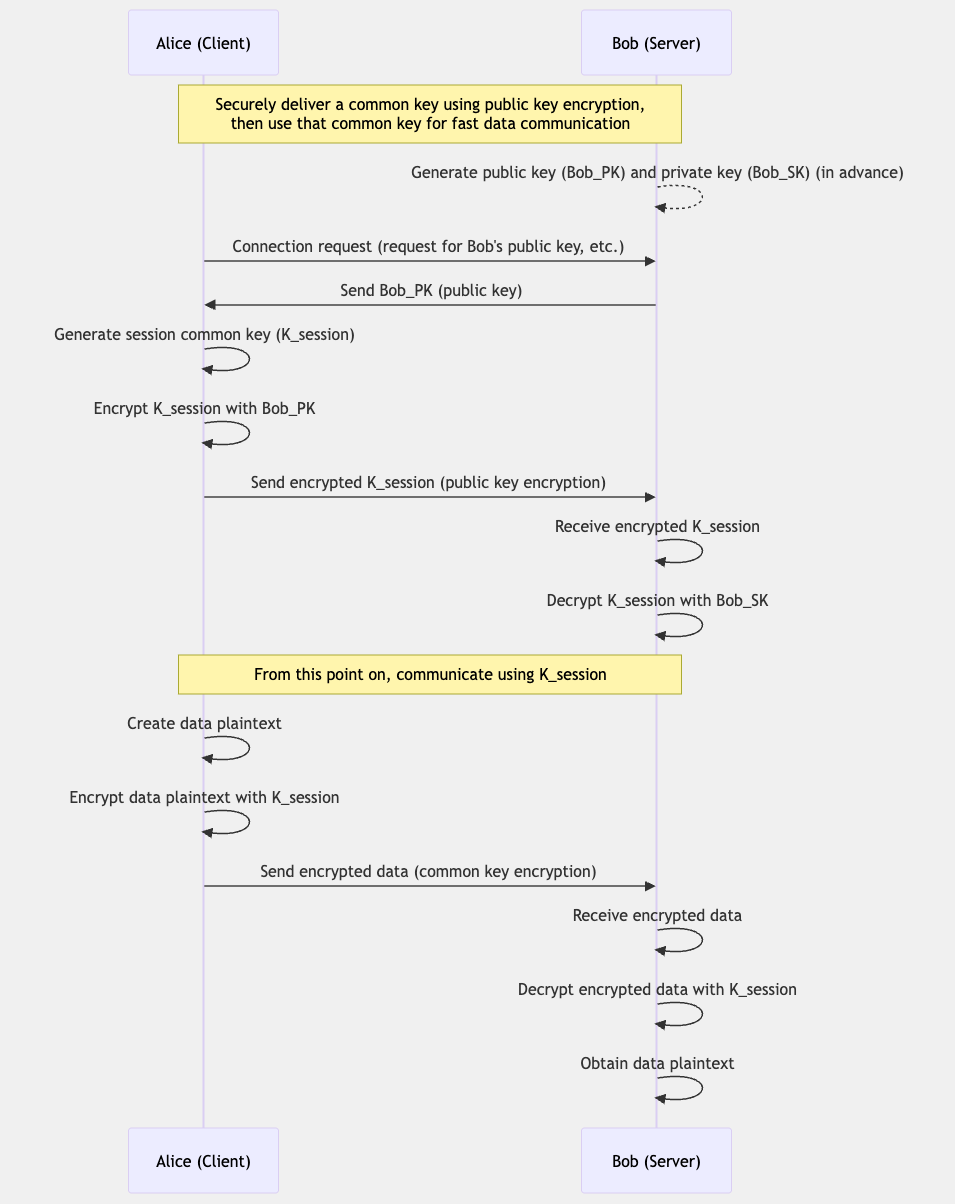
This approach achieves both the secure key exchange of public-key cryptography and the high-speed processing of symmetric-key cryptography. Many modern encryption protocols, such as TLS/SSL, PGP, and S/MIME, employ a hybrid system.
Applications of Encryption Keys
Encryption keys are used in various situations in modern digital society. The main application examples are as follows:
- About SSH Connections
- Web Security: HTTPS communication, SSL/TLS certificates
- Email Security: Encryption and signatures with S/MIME, PGP
- Digital Signatures: Signing electronic documents, code signing
- Authentication Systems: Storing passwords, multi-factor authentication
- Data Protection: Disk encryption, file encryption
- Secure Communication: VPN, wireless communication (WPA2/WPA3)
- Blockchain Technology: Cryptocurrency wallet management